Продолжение. Немного теории.
Электрет. Что это такое, как получается, как используется.
Электреты — это диэлектрики, длительное время сохраняющие поляризованное состояние после снятия внешнего воздействия, вызвавшего поляризацию, и создающие электрическое поле в окружающем пространстве (электрические аналоги постоянных магнитов).
Если вещество, молекулы которого обладают дипольным моментом, расплавить и поместить в сильное электрическое поле, то его полярные молекулы частично выстроятся по полю. При охлаждении расплава в электрическом поле и последующем выключении поля после затвердевания вещества поворот этих молекул затруднён и они длительное время сохраняют преимущественную ориентацию (от нескольких дней до многих лет). Первый электрет был таким методом изготовлен М. Ёгучи (М. Eguchi) в 1922 году. [1,2]
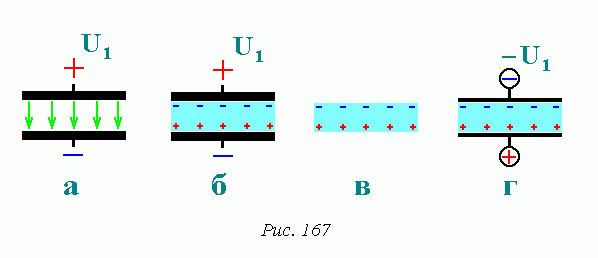
Возьмем плоский конденсатор (рис. 167 а), его емкость прямо пропорциональна площади пластин и обратно пропорциональна расстоянию между ними [3]:
.  . . . . . . . . . . . . . . . {1}
. . . . . . . . . . . . . . . {1}
Где С — емкость в Фарадах, eo — электрическая постоянная, размерность Фарад/метр (eo примерно равнa 8,85*10-12), e — относительная диэлектрическая проницаемость (безразмерная), S — площадь пластин конденсатора, метр2, d — расстояние между пластинами, в метрах.
Если такому конденсатору сообщить заряд Q, то на нем появится напряжение
.  . . . . . . . . . . . . . . . . . . {2}
. . . . . . . . . . . . . . . . . . {2}
Q — заряд в Кулонах, напряжение в Вольтах, емкость в Фарадах.
Напряженность поля между пластинами будет E=U/d.
Заметим, что напряженность электрического поля прямо пропорциональна напряжению между пластинами и обратно пропорциональна расстоянию между ними и не зависит от диэлектрической проницаемости диэлектрика между пластинами (при прочих равных условиях, т.е. U=const).
Теперь, если между пластинами конденсатора мы зальем расплавленный диэлектрик, напрмер политетрафторэтилен, и дадим ему затвердеть, то поляризовавшийся под действием электрического поля диэлектрик, сохранит свою поляризацию после снятия напряжения с конденсатора, сохранит ее даже после изъятия диэлектрика из конденсатора. Рис. 167 б, в.
Если же мы вставим поляризованный диэлектрик (электрет) между пластинами другого, разряженного конденсатора, то под действием поля диэлектрика, пластины конденсатора поляризуются, причем таким образом, что на выводах конденсатора появится напряжение равное напряжению поляризации (для идеального электрета), но противоположное по знаку. Рис. 167 г.
Вспомним, как устроен электретный микрофон (см. предыдущий пост) рис. 168 а.
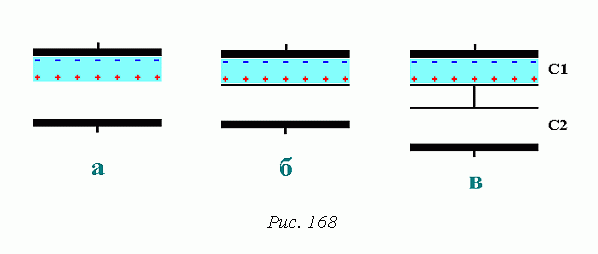
Сверху вниз: электрод, электрет, воздух, электрод.
Поскольку нижнюю поверхность электрета, в первом приближении, можно считаль эквипотенциальной, на границе раздела сред электрет — воздух, мы можем ввести электропроводную поверхность и это не повлияет на конфигурацию электрического поля между верхним и нижним электродами (рис. 168 б). Тогда мы можем представить введенную поверхность как два электрода, электрически соединенные между собой (рис. 168 в). С точки зрения физики, эти преобразования вполе корректны.
Таким образом, у нас получились два последовательно соединенные конденсатора, причем, верхний, с электретом между обкладками (С1), будет иметь постоянню емкость, поскольку толщина электрета не меняется, а емкость нижнего конденсатора, с воздушным диэлектриком (С2), будет меняться при колебании мембранки. Важно заметить, что верхняя обкладка конденсатора С2 всегда будет заряжена до напряжения U относительно верхней обкладки С1. Если же мы замкнем верхний вывод С1 и нижний С2, то и относительно нижней обкладки С2 тоже.
Итак, у нас есть конденсатор с воздушным диэлектриком С2, заряженный до напряжения U и с изменяемой пропорционально смещению мембранки емкостью, конденсатор С1 с функциональной точки зрения нас не интересует, поскольку напряжение на нем не меняется, как и его заряд. По какому закону будет меняться напряжение на С2 при изменении расстояния между его пластинами ?
Напряжение на конденсаторе U=Q/C, подставив в {2} формулу {1}, получим:
.  . . . . . {4}
. . . . . {4}
Чтобы не загромождать выкладки введем обозначение:
 , тогда
, тогда  , очевидно:
, очевидно: 
Относительное изменение напряжения :  . . . . . . . {5}
. . . . . . . {5}
Заметим, что выражение {5} не зависит от емкости и выполняется для любой емкости.
Из приведенных выше формул есть несколько интересных следствий:
1. Из {4} следует, что напряжение ма конденсаторе С2, а следовательно и на самом микрофоне прямо пропорционально расстоянию между пластинами, т.е. зависимость ЭДС микрофона от смещения мембранки строго линейная!
2. Из {5} следует, что относительное приращение напряжения на конденсаторе С2 , а это и есть, по сути, ЭДС микрофона, не зависит от емкости микрофона. Емкость микрофона влияет только на мощность сигнала, выдаваемого микрофоном.
Практически это означает, что при напряжении на конденсаторе 100 Вольт и смещении мембранки на 1% (при зазоре 30 мкм — 1% — это 0,3 микрона!) на выходе получается ЭДС 1 Вольт. Если смещение мембранки зафиксировать, то на выходе микрофона будет постоянное напряжение 1 Вольт (без учета потерь из-за разряда емкости через входное сопротивление усилителя).
Для микрофона с электретом на неподвижном электроде принципиально ничего не меняется, надо только поменять местами С1 и С2.
Таким образом, электретный микрофон сам по себе ничего не дифференцирует, напряжение на его выходе прямо пропорционально линейному смещению мембранки, независимо от частоты.
_________________________________________________________
В отличии от электретных, динамические микрофоны, в принципе, дифференцируют входной сигнал, поскольку ЭДС таких микрофонов пропорциональна скорости движения катушки, т.е. первой производной по перемещению.
[1] http://www.heuristic.su/effects/catalog … index.html
[2] http://dic.academic.ru/dic.nsf/enc_phys … /ЭЛЕКТРЕТЫ
[3]_http://www.fxyz.ru/формулы_по_физике/электричество/электрическое_поле/электрическая_емкость/конденсатор/плоский_конденсатор/емкость_плоского_конденсатора/
= www.fxyz.ru
_http://fablabs.ru/wiki/index.php/Электрет = Ссылка












 Не то что Биомедисы стоят. Ого-гошеньки!
Не то что Биомедисы стоят. Ого-гошеньки!














 . . . . . . . . . . . . . . . {1}
. . . . . . . . . . . . . . . {1} . . . . . . . . . . . . . . . . . . {2}
. . . . . . . . . . . . . . . . . . {2}
 . . . . . {4}
. . . . . {4} , тогда
, тогда  , очевидно:
, очевидно: 
 . . . . . . . {5}
. . . . . . . {5}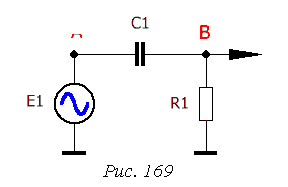
 и частоту среза фильта
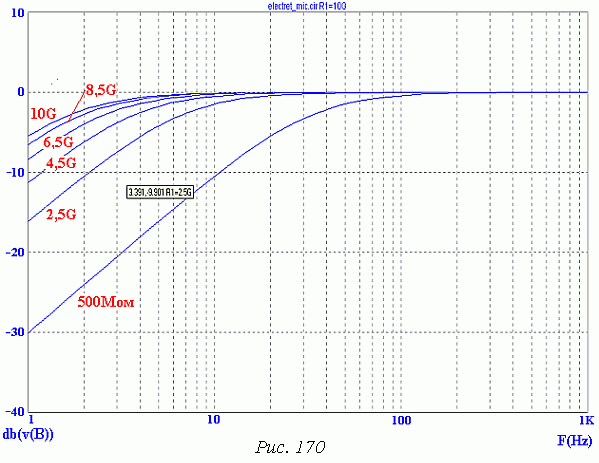
и частоту среза фильта  [1]. Как и всякий фильтр, образованный одиночной RC-цепочкой — она дает спад АЧХ на частоте ниже частоты среза примерно на 6 децибел на октаву, т.е. каждое снижение частоты вдвое уменьшает амплитуду сигнала в 2 раза.
[1]. Как и всякий фильтр, образованный одиночной RC-цепочкой — она дает спад АЧХ на частоте ниже частоты среза примерно на 6 децибел на октаву, т.е. каждое снижение частоты вдвое уменьшает амплитуду сигнала в 2 раза.